新闻活动

点击跳转公众号原文：基于3D数字图像相关测量实验数据与仿真数据互验的全场方法论

或直接观看B站视频解说：

本文旨在系统阐述基于3D-DIC实验数据与仿真数据互验的全场方法论，共分为五个部分：

① 背景介绍

② 全场数据耦合与比对

③ DIC数据与FEA结果精确对比

④ DIC与FEA应力分析

⑤ 总结与意义

 01 背景介绍

· 有限元分析（FEA）是预测复杂物理现象的核心手段，但其准确性依赖边界条件、载荷和材料属性等多种因素，需与实验数据结合验证。

· 传统对比方法多为全局轮廓对比，缺乏点对点的定量分析，难以精准识别局部差异，尤其在材料发生弹塑性变形的关键区域。

· 各向异性材料（如轧制铝合金）的力学响应模拟存在挑战，需优化屈服准则以提升仿真精度，反演材料真实应力分布。

面对这样的问题，将有限元分析结果与高置信度实验数据结合进行严格验证是合理有效的解决方案，不仅能通过实验数据为仿真提供指导方案，同时仿真结果也能反馈指导实验设计。

数字图像相关技术(Digital Image Correlation, DIC)概述

以被测对象表面随机分布的散斑场构建测量特征，使用各种图像采集硬件捕捉散斑场在变形过程的数字图像序列，通过优化的2D或3D数字图像相关算法的后处理，获取被测对象在二维或三维空间的全场数据形态的形貌、位移及应变等数据的非接触式图像测量方法。

在上述背景下，DIC技术有不可替代的应用优势。它采用非接触式测量方法，提供了传统方法难以企及的全场、高分辨率变形数据：

· 能为FEA提供海量可直接点对点比对的数据源，实现从“宏观轮廓符合”到“微观数据对标”的跨越；

· 对局部应变集中等现象极为敏感，可为FEA模型在关键区域的预测偏差提供修正依据；

· 将材料模型反演从“曲线拟合”问题提升到了“物理场重构”问题，即便对于具有复杂非线性、各向异性行为的先进本构模型，也能精确描述。

因此，基于3D-DIC实验数据与FEA仿真数据的互验，构成了解决前述挑战的全场方法论核心。

 02 全场数据耦合与比对

这一部分的三项内容共同构成了从“有两组数据”到“能进行科学对比”的技术桥梁。核心目标是将实验测量的离散点云数据（DIC）与仿真的网格节点/积分点数据（FEA）在同一个参考系和相同的空间位置上进行比较。

 Step1、空间坐标统一理论

基于刚体变换（旋转矩阵 + 平移向量）实现DIC与FEA坐标系的精准对齐，核心依据是 continuum mechanics 理论的矢量与张量变换规则。这一步的作用在于消除系统性的位置和方向偏差，并为后续比对建立共同基准。针对不同情况下的试样，这里分享三种对齐方法：

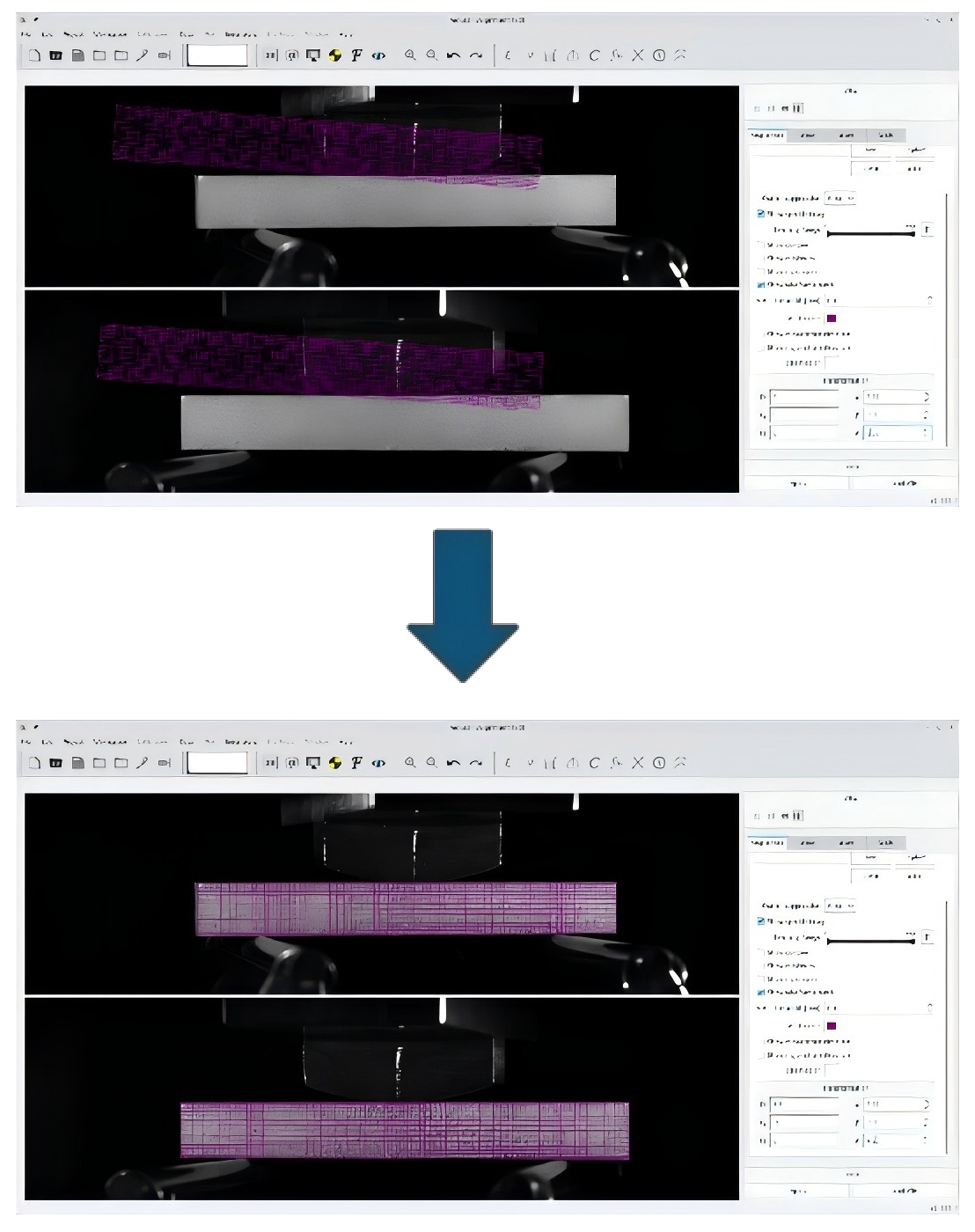
在 VIC-3D 中支持模型的旋转/平移调整

· 基于特征提取的对齐方法

利用试样特征点的三维空间坐标匹配模型中对应特征点的坐标，求解并利用变换参数将所有 FEA 节点坐标和物理场数据转换到实验坐标系。

✔ 适用于试样本身具有明确自然特征的情况（如缺口、棱角、界面等）。

· 基于表面标记的对齐方法

在试样表面标记点，利用标记点的三维坐标，采用与特征提取法相同求解逻辑，完成坐标系统一。

✔ 适用于试样表面无明显自然特征，或自然特征难以精准识别的情况。

· 基于点云配准的对齐方法

利用 FEA和DIC 的三维点云数据；以DIC点云为参考坐标系，采用快速点特征直方图（FPFH）算法和迭代最近点（ICP）算法求解变换参数并应用于 FEA 数据，实现坐标统一。

✔ 需要更高自动化程度和对齐精度，或试样表面特征复杂的情况。

 Step2、全场差值理论

全场差值理论有效克服了传统全局对比所存在的局限性，达成对数据的点对点定量分析。该步骤的核心意义在于妥善处理数据空间位置不匹配的问题，从而保障对比的合理性以及分析结果的精度。

· 采用重心坐标插值法，将 FEA 网格数据映射至 DIC 测量点，确保不同空间离散度数据的可比对性。

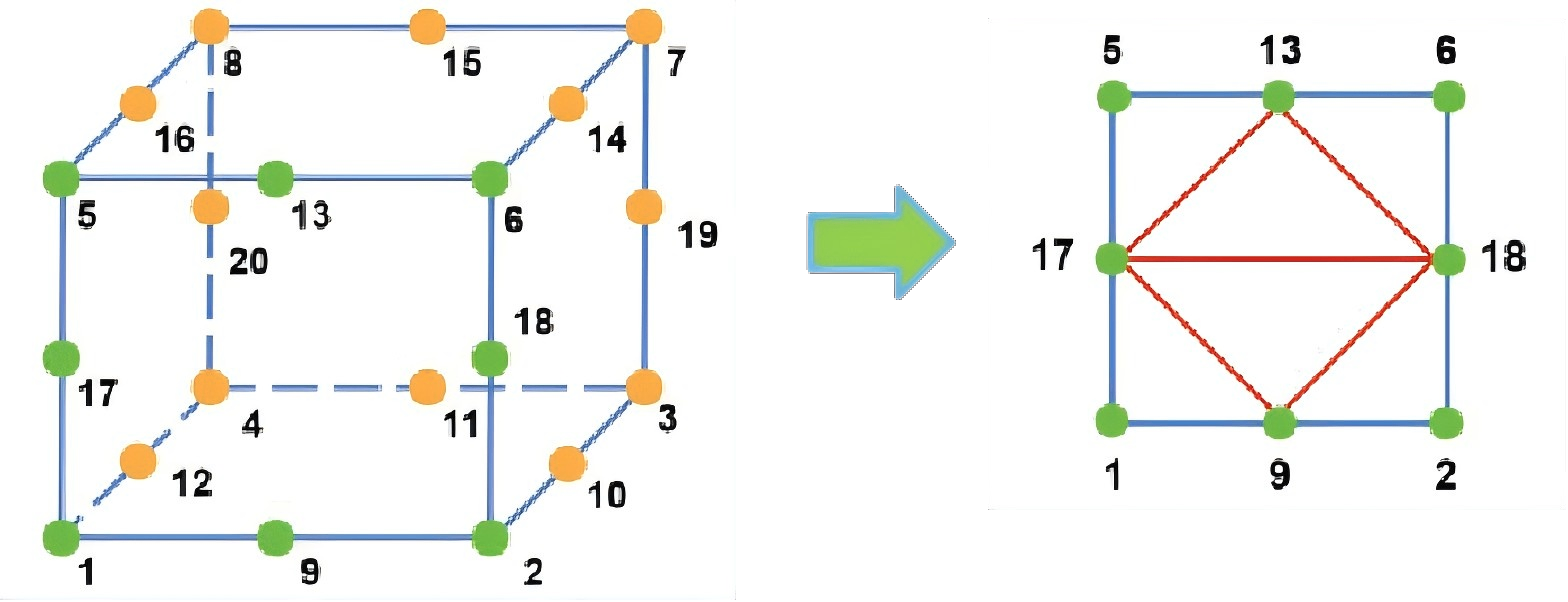
有限元单元网格三角化

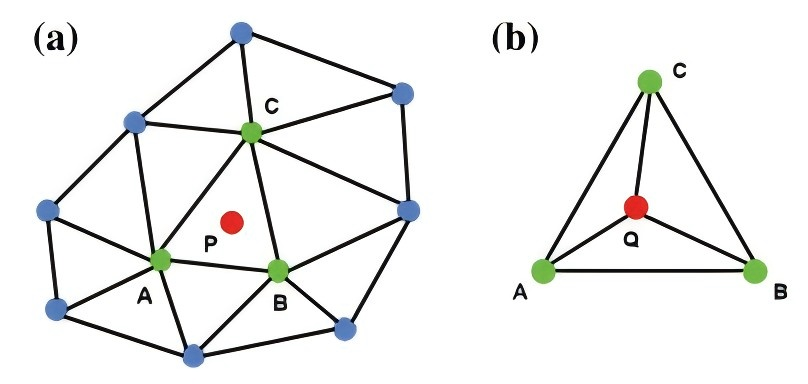
DIC数据点(红色)与FEA网格(绿色)

· 将有限元分析数据导出/转换为DIC工作区支持的格式：三角形网格与场变量数据（VTP格式）。

· 量化分析：建立三级误差评估体系（全场平均误差、局部峰值误差、关键区域方差），精准定位差异分布。

Step3、实验测值与FEA预测值在相同空间位置上的差值计算

在完成了空间坐标统一与数据插值，确保DIC实验数据与FEA仿真数据能在同一空间位置进行“点对点”对比后，差值计算这一步便成为了整个互验流程的核心。它远不止于简单的数学相减，而是一个层层递进的深度分析过程：

· 首先，差值计算的有效性建立在三大基础之上： 准确的边界条件设定、精确的空间坐标统一以及合理的数据离散度适配。

· 然后，进行“误差溯源”。通过系统性地排除实验测量噪声、网格离散误差及坐标对齐残余偏差等非模型因素，确保最终观测到的差值根源能更纯粹地指向FEA模型本身的不足。这为后续的模型修正锁定了明确方向。

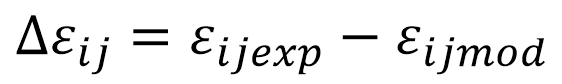
应变差值为 DIC 实验测量与FEA应变的差值

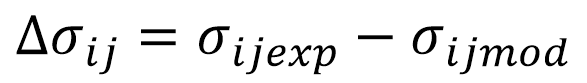
需基于相同的屈服准则（如 Hill 二次各向异性屈服准则）分别从 DIC应变反演应力从有限元模型提取应力再进行差值计算

· 进而，通过比对材料在不同屈服准则下仿真与实验的全场应变差值云图及分布特征，以此定量且直观地判断本构模型的适配性。这直接揭示了本构模型与真实材料各向异性行为差异的本质，让模型选择有据可依。

· 最终，这一切都服务于优化与校准本构模型的终极目标。 差值计算能够指导应力场反演，并将反演结果与仿真应力场进行比对。

这一过程为优化校准材料模型提供了海量的全场数据目标，驱动其自动调整材料模型参数，直至FEA的预测与DIC的实验测量在全局和局部上都实现高度吻合，从而校准出能够真实反映材料行为的精准模型。

03 DIC数据与FEA结果精确对比

这里通过一个预浸料薄复合带屈曲实验的具体案例，来展示DIC数据与FEA结果精确对比的操作流程。

为什么选择该案例？

高性能复合材料领域，如飞机机翼、赛车车身和风力涡轮机叶片等部件的制造中，预浸料薄复合带因其卓越的强度-重量比和抗疲劳性能而被广泛应用。然而，这种薄壁结构在受力时极易发生复杂的屈曲行为，对其进行精准预测是结构设计的关键。

预浸料薄复合带

屈曲这种涉及整体失稳、形态复杂的现象，单点测量完全无法捕捉其全场变形特征。DIC能够提供与FEA结果在数据形态上完全一致的全场位移与应变云图，是进行此类验证的首选方法。二者的数据可以进行直接的、像素到节点的定量对比。

具体操作流程：

（1）对齐坐标系

结果匹配是极其重要的程序，这里采用特征点标记法这一最可靠的方式，通过VIC-3D 软件自动识别标记并计算坐标变换矩阵，将所有 DIC 数据统一到FEA模型的坐标系下，为后续点对点对比扫清根本障碍。

· 对于外形规则的试件，可以直接利用其整体轮廓定义AOI边界进行匹配；

· 也可以利用物体表面三个不共线的自然特征（如边角、小孔）确定特征点，通过“三点定坐标系”的原理手动实现对齐。

试件固定与标记

（2）导入有限元数据

· Abaqus FE model using 8-node thick shell elements (S8R) 

建立基于Abaqus的有限元模型，使用8节点厚壳单元（S8R）进行模拟。

· 定义边界条件：固定试件左侧，右侧施加位移载荷。该载荷直接取自DIC实测数据，这确保了仿真与试验的输入条件完全一致。

· 使用Python脚本从Abaqus中导出五个加载步下的有限元结果，并导入到VIC-3D软件中。

· 同时，为确保实验与仿真数据在同等条件下进行比对，需要进行精心的分析参数匹配：在DIC分析中，设置与FEA网格尺寸相协调的应变过滤器大小，以获得最佳比较结果。

这一步至关重要，它消除了因数据平滑度不同带来的非物理误差，确保后续看到的差值是真正源于模型预测与物理现象之间的偏差。

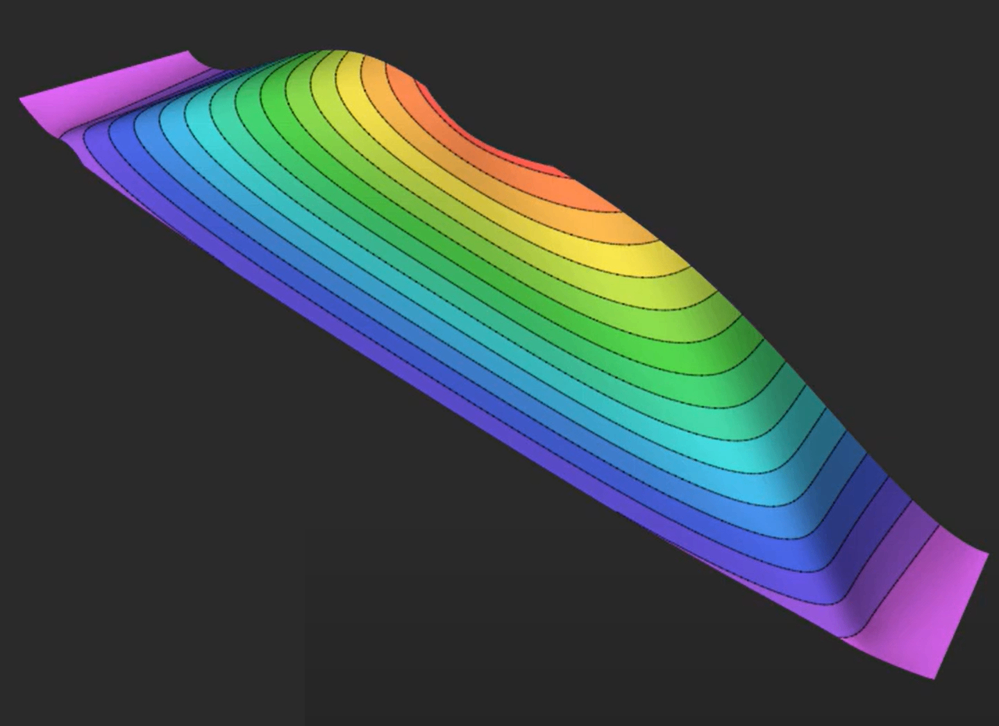
试件有限元模型

（3）DIC与有限元数据差值运算

使用 python 脚本从 DIC 中减去 Abaqus 数据，执行全场数据的核心差值运算。该过程首先进行空间坐标匹配：采用kD-Tree 算法，对每一个DIC数据点执行快速的局部邻域搜索，高效且精准地定位DIC数据点在有限元网格中空间上最邻近的节点，以此有效确定近似对应关系。

随后算法进一步确定DIC数据点在有限元网格单元内的具体位置，并利用该单元的形函数，插值计算出与DIC数据点空间位置匹配的FE预测值；最终通过逐点相减（Δ = DIC测量值 - FE预测值），生成全场的定量误差分布云图。

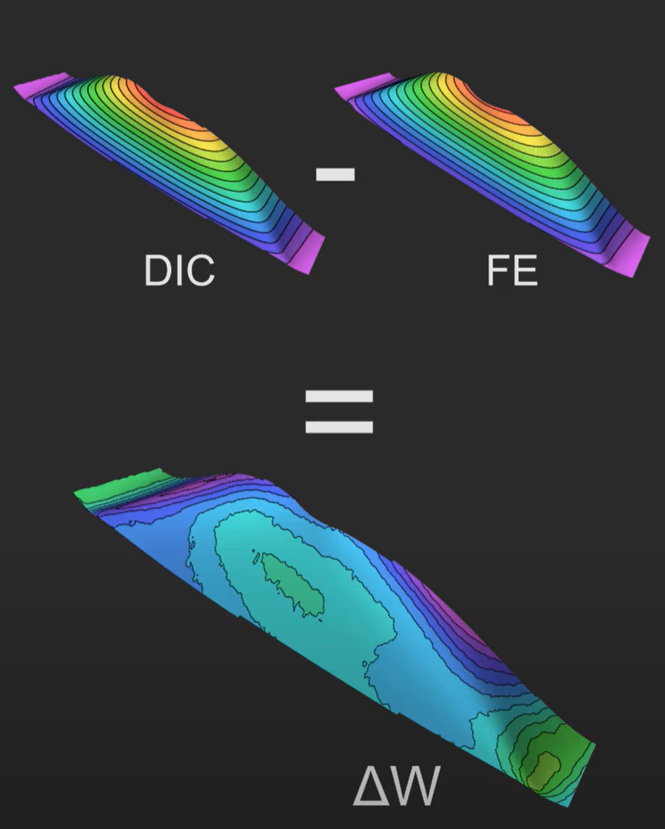
DIC与有限元数据差值计算

 （4）结果及高质量可视化呈现

（可从视频03:00开始观看数据变化云图）

04 DIC与FEA应力分析

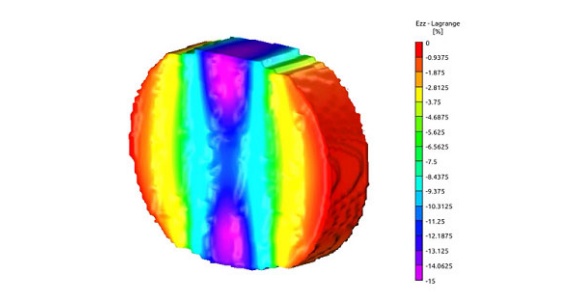
在上一步DIC数据与FEA结果的精确对比阶段，通过全场位移和应变的差值计算，得到清晰的误差分布云图。这些云图不仅能精确指出“哪里不一致”，还能定量的给出“差异有多少”。而应力分析在这个基础上将实验与仿真的互验推向了更深层次，直接涉及到材料行为与本构模型的差异关系。这不仅回答了“模型是否准确”，更揭示了“模型为何不准确”以及“如何改进”。

在有限元中施加来自于实验的位移边界条件：

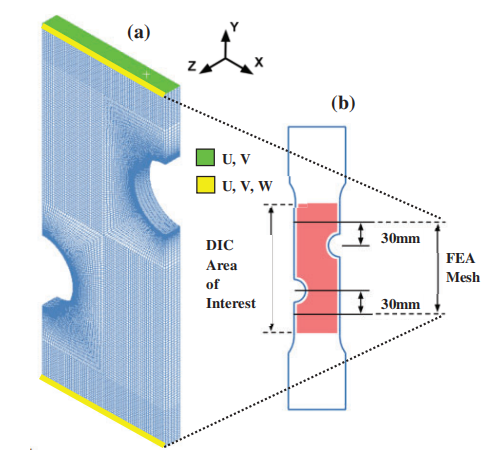
(a) 有限元分析网格，其顶部和底部施加了U、V（绿色区域）及U、V、W（黄色线）位移的边界条件；(b) 试样几何结构及有限元模型中DIC关注区域（红色标注）

直接在有限元模型中施加以DIC全场位移测量结果为基础的边界条件。这最大限度地保证了仿真与实验边界条件的一致性，使后续差异来自于材料模型。

DIC后处理中采用有限元相同的材料模型准则分析应力：

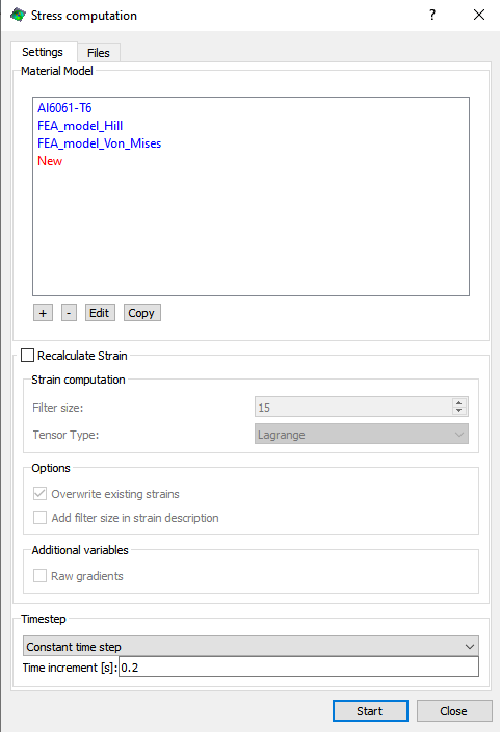
应力分析模块

在DIC后处理中，启用应力分析模块，该模块的功能在VIC-3D 10中得到极大更新。此模块的强大之处在于，它不仅能对DIC与FEA的应力场执行同样精细的全场差值运算，更核心的是，它支持多种材料模型，并允许用户通过直观的对话框或标准化的JSON文件便捷地定义复杂模型。最关键的一点在于，可以在此模块中直接调用与有限元仿真完全相同的材料模型。

这一设定确保了实验与仿真站在同一物理定律的起跑线上，使得任何观测到的应力差异都来自于材料行为或本构模型参数，而非比较基准不一。最终，整个 “分析、保存、共享、重复” 的流程，将应力对比从一次性的验证，升级为一个可迭代、可优化的标准化工作流，为精准反演材料参数提供了高效且可靠的平台。

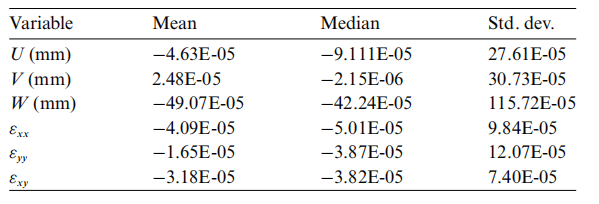
DIC分析位移应变的误差

利用相同材料模型处理的DIC应力场与FEA结果对比：

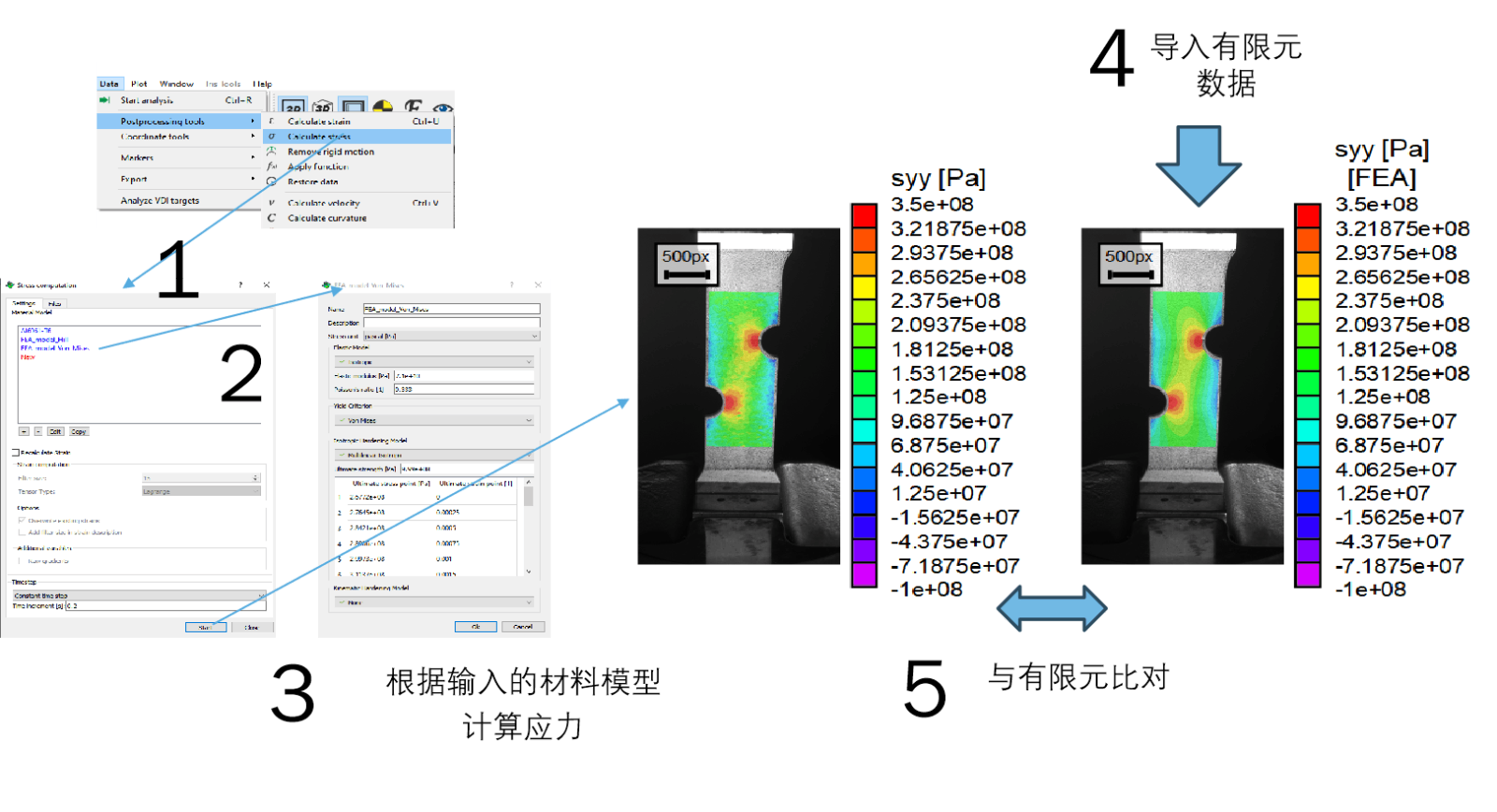
结果对比操作流程

DIC与有限元应力演变结果

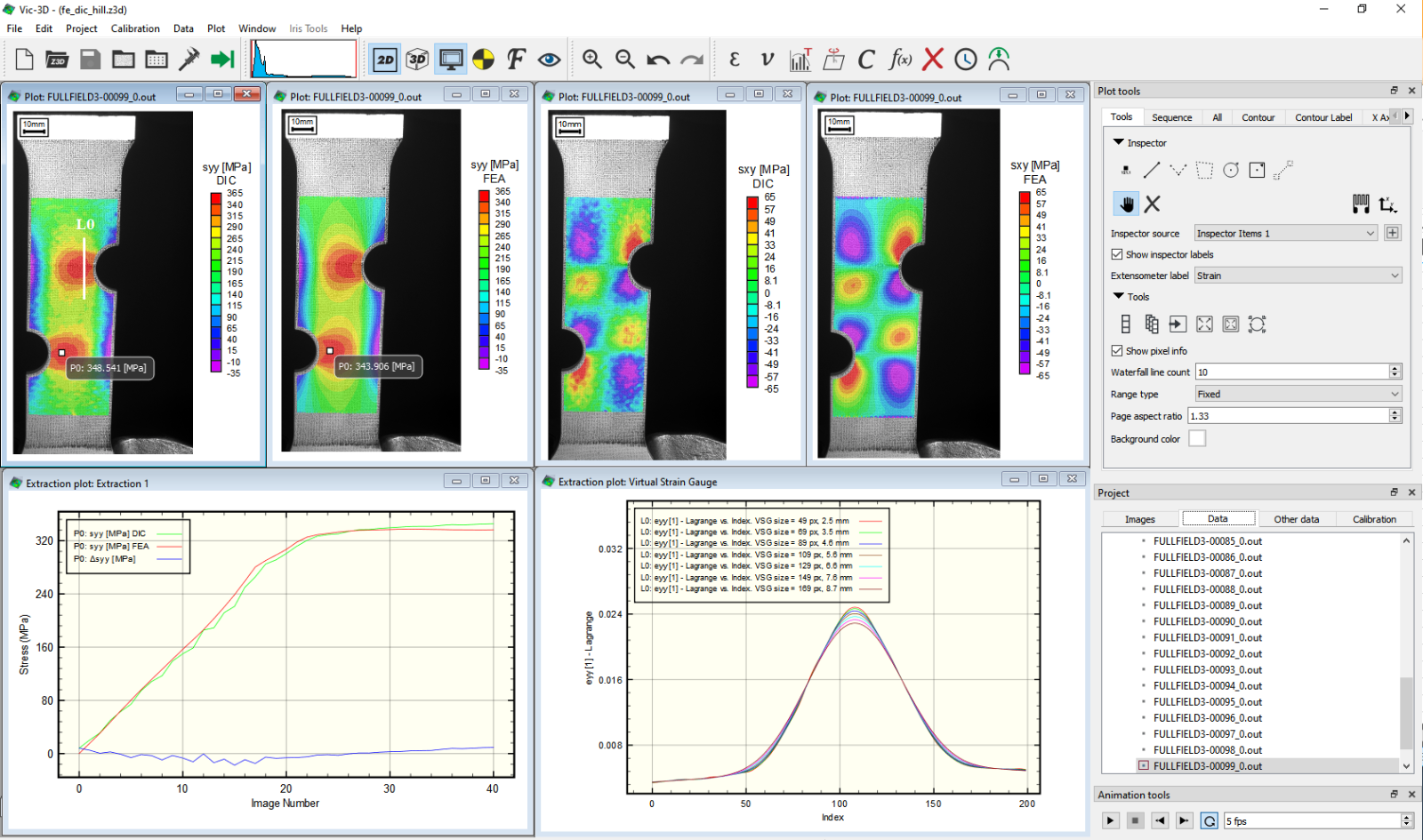
DIC数据与有限元结果的可视化及定量对比

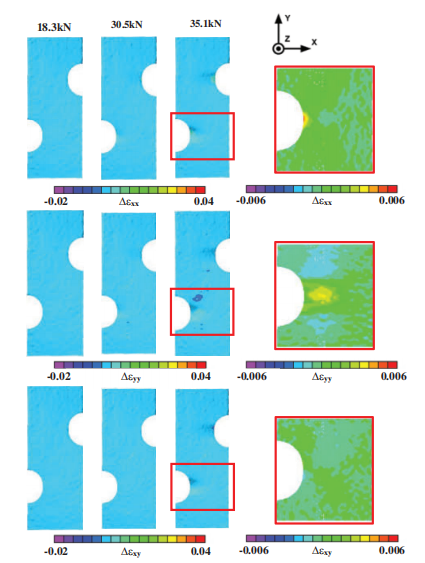
DIC与有限元结果在不同载荷下的对比差异

DIC数据与有限元结果在缺口处的应变差异：

排除实验测量误差后，实验数据与有限元结果表明，有限元预测值与DIC测量值在局部塑性变形前（弹性阶段）的吻合度较高，但在塑性变形（弹塑性阶段）区域的吻合度明显下降。

这一现象明确指示：当前FEA所使用的材料模型无法准确描述材料在弹塑性阶段的真实行为。究其原因，很可能是实验材料在加工过程中产生了制造变形，可能导致各向异性响应（例如长度、宽度和厚度方向的屈服应力可能不相等）。

本构模型的筛选与优化：

DIC数据与有限元结果对比的最终价值，在于其差值可作为本构模型优化的量化依据。

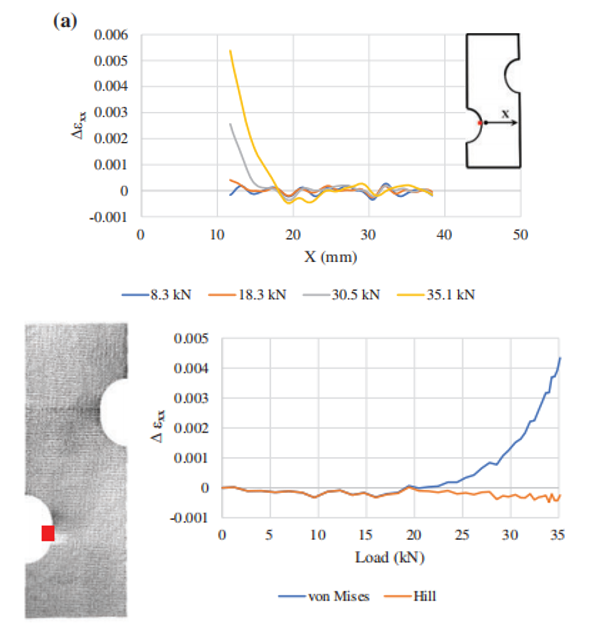
不同屈服准则的对比结果

对比von Mises（各向同性） 和Hill（各向异性） 两种屈服准则，结果表明，低载荷(弹性阶段)，两种准则计算的DIC与FEA差距均较小，高载荷(塑性阶段)下，Hill准则在减少DIC与FEA误差上具有更大优势，后者可以充分体现DIC实验数据与FEA在对各向异性材料定量表征的统一，Hill准则表征缺口区域塑性误差降低 80%。

模型的优越性需要最严格的定量考核。可以通过一些关键指标对优化后的模型进行最终验证。

缺口应力集中系数公式：

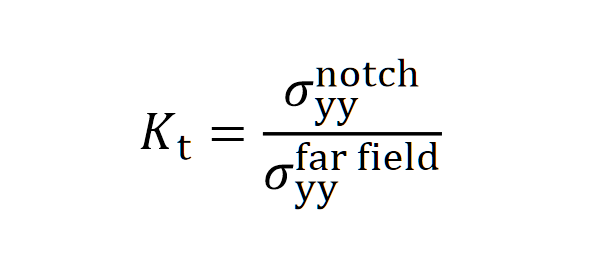
实验与有限元的缺口敏感系数公式：

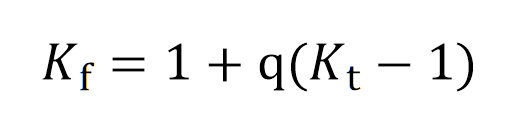
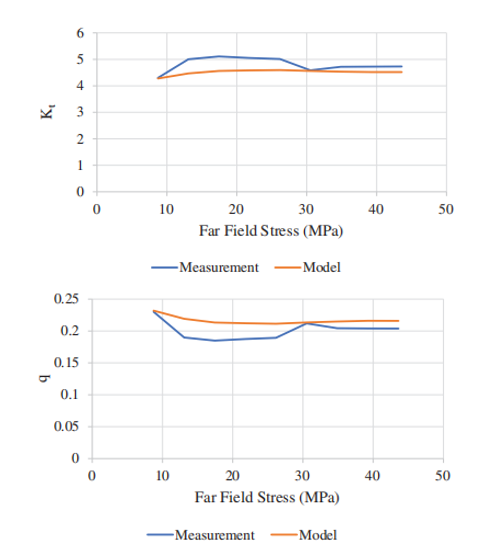
缺口参数对比，高度一致：这表明优化后的模型，对材料行为的表征不仅在“面”上（全场）整体吻合，在“点”上（最复杂、最关键的局部）也极为精确。

05 总结与意义

基于VIC-3D软件的iris三维数据图形引擎构建实验与仿真数据互验的全场方法论，实现了DIC试验测量数据与有限元（FE）预测结果在统一空间坐标系下的精准对比，包括：

· 数据空间对齐‌：通过Python扩展模块将有限元表面离散化网格转换为结构化三角网格，建立全场物理量插值基础框架；

· 跨平台数据耦合‌：基于公共空间坐标节点，实现有限元预测场量（应力/应变）与DIC实验测量数据的逐点映射对比；

· 仿真对标设置‌：在有限元环境中采用实测端点位移边界条件进行数值模拟，确保与实验工况严格对应；

· 材料各向异性定量表征‌：基于自主研发的逐点对比分析方法；

· 本构模型优化验证了逐点对比度量方法在材料模型校准中的关键作用；

· 全场应力重构技术实现基于VIC-3D全场应变数据与先进材料模型的全流程应力场反演。

技术价值：

· 解决 “空间错位 - 数据失配” 核心矛盾，实现精准量化对比

通过刚体变换坐标对齐和重心坐标全场插值技术，将 FEA 数据精准映射至 DIC 测量点，实现 “点对点” 空间统一。

· 构建 “误差溯源 - 模型优化” 闭环，提升仿真可信度

精确定位误差来源：材料本构模型适配性问题；FEA 网格密度问题；坐标对齐精度问题。

· 拓展 “实验反哺仿真” 能力，实现本构模型与边界条件双优化

通过全场数据差异对本构模型参数优化；FEA边界条件真实化。

工程意义：

· 为高应力结构提供 “精细化验证” 方案，降低失效风险

通过全场应力重构技术（基于 DIC 应变与 Hill 准则反演应力），无需依赖 FEA 即可获得局部高应力区域的应力分布。

· 推动复合材料、动态载荷等复杂场景的力学验证标准化

通过 DIC 测量应变与 FEA 对比，验证各向异性材料的弹性模量匹配性。通过 DIC 测量的应变率FEA 动态本构模型对比，修正应变率敏感参数等。

· 降低 “实验 - 仿真” 耦合门槛，推动工程验证效率提升

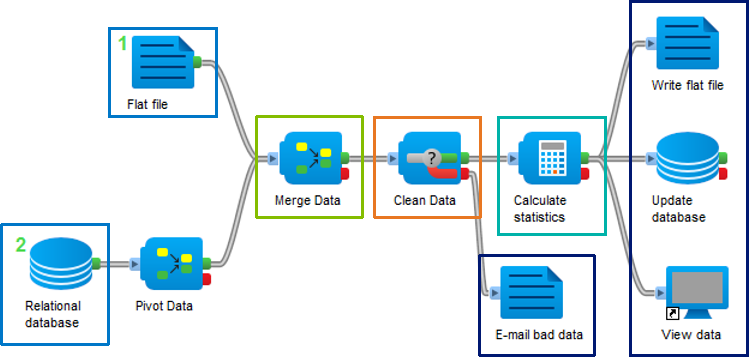
通过脚本工具实现 “数据转换 - 坐标对齐 - 差值计算 - 可视化” 全流程自动化。

行业学术意义：

· 学术层面：完善 “实验 - 仿真” 互验理论体系

明确了不同坐标对齐方法的适用边界；提出 “本构模型 - 误差分布” 关联规律。

· 行业层面：助力 “数字孪生” 与 “智能制造” 落地

数字孪生需将物理实体的力学状态与虚拟模型对标，该方法论提供了 “数据互验” 的核心技术。

研索仪器基于DIC技术的VIC-3D非接触全场测量系统，是来自于全球DIC理论与技术的原创者和领导者——Correlated Solutions公司的科研级DIC测量解决方案，40多年的深耕，造就了VIC-3D系列解决方案卓越且领先于行业的高精度、高稳健性、环境适用性、功能扩展性和极高的计算效率。

如果您对该项技术或相关方法论感兴趣，欢迎随时与我们联系。